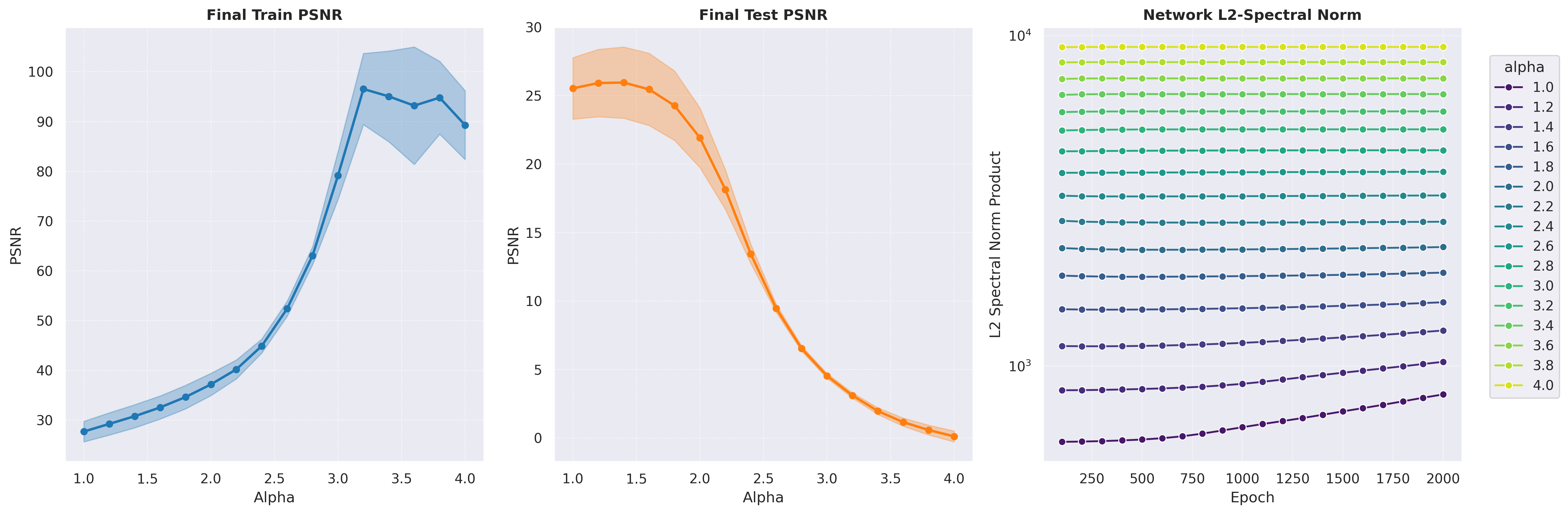
Implicit Neural Representations (INRs) have shown great promise in solving inverse problems, but their lack of inherent regularization often leads to a trade-off between expressiveness and smoothness. While Lipschitz continuity presents a principled form of implicit regularization, it is often applied as a rigid, uniform 1-Lipschitz constraint, limiting its potential in inverse problems.
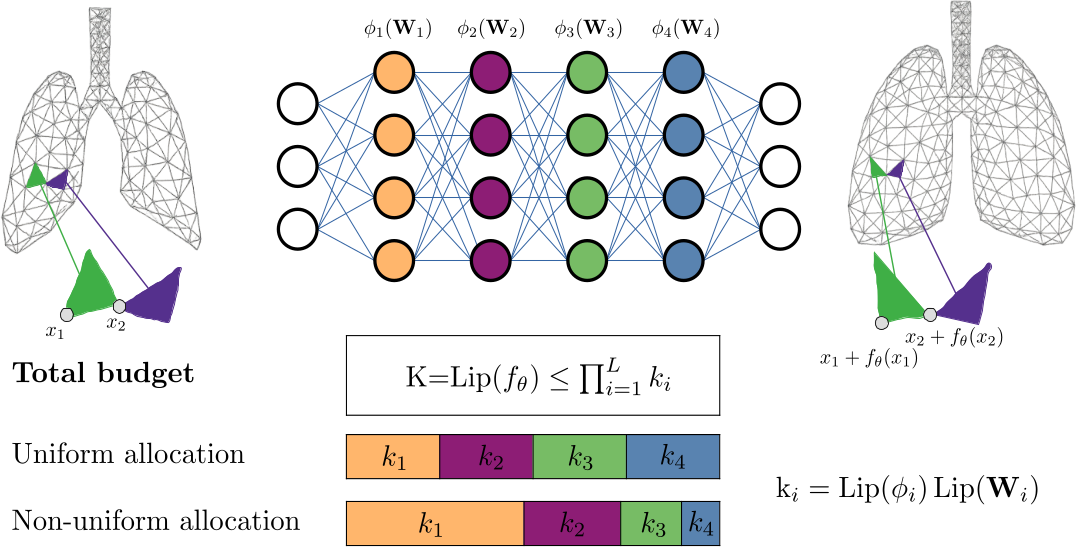
In this work, we reframe Lipschitz regularization as a flexible Lipschitz budget framework. We propose a method to first derive a principled, task-specific total budget K, then proceed to distribute this budget non-uniformly across all network components, including linear weights, activations, and embeddings.
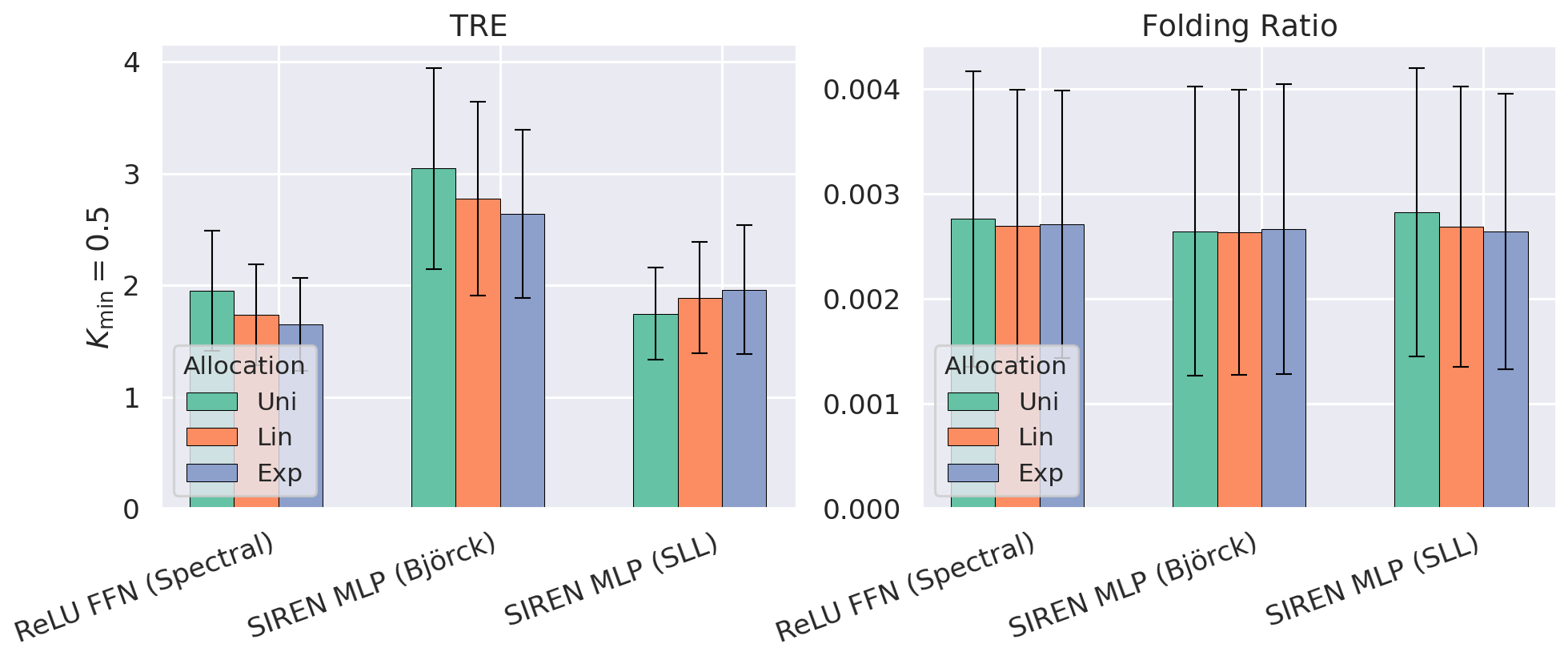
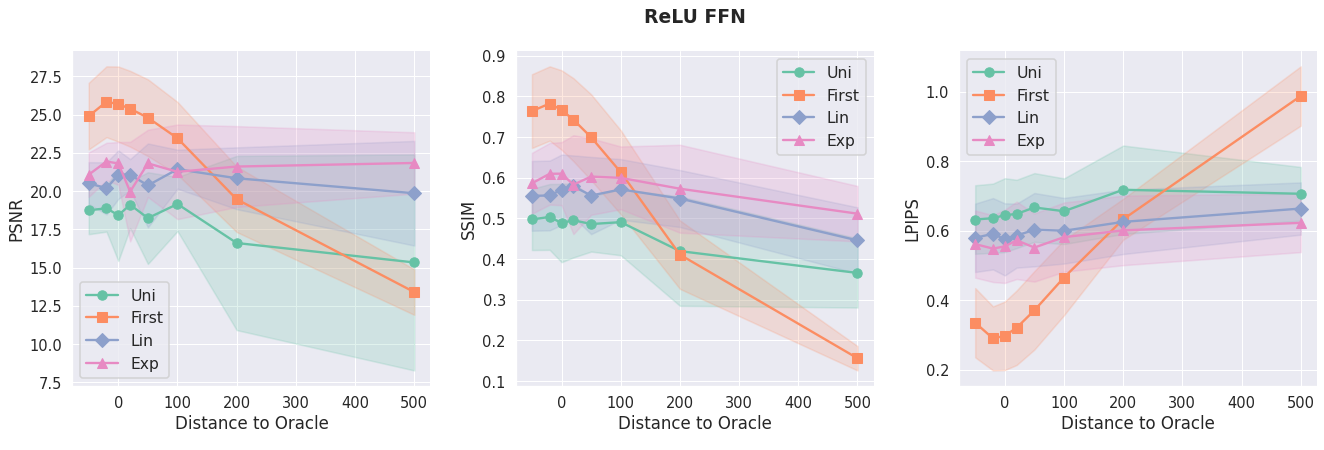
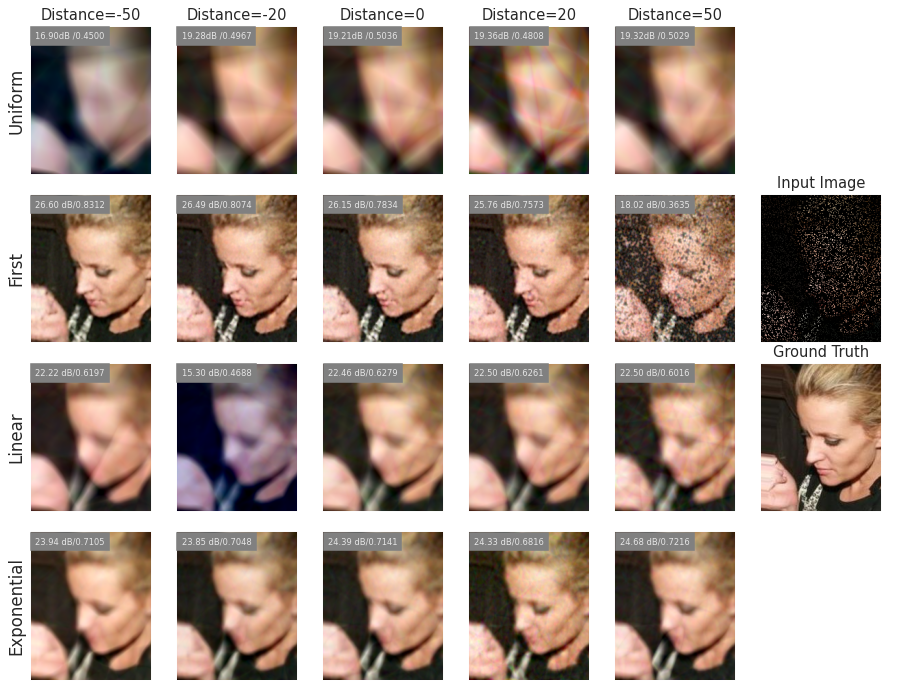
Across extensive experiments on deformable registration and image inpainting, we show that non-uniform allocation strategies provide a measure to balance regularization and expressiveness within the specified global budget. Our Lipschitz lens introduces an alternative, interpretable perspective to Neural Tangent Kernel (NTK) and Fourier analysis frameworks in INRs, offering practitioners actionable principles for improving network architecture and performance.
For a network \(f_\theta\) with L layers, the overall Lipschitz constant K is bounded by the product of individual layer and activation Lipschitz constants:
This compositional property reveals that a global budget K can be achieved through various combinations of layer-wise constants, motivating our exploration of different budget allocation strategies.
Given the total Lipschitz budget \(K_B\), we investigate multiple allocation strategies:
We investigate how different spectral normalization techniques and gradient-preserving activation functions affect SDF learning quality. Our key finding: approaching the upper Lipschitz bound correlates with better perceptual quality.
Learning the Stanford bunny with different spectral normalization techniques (first row) and different gradient-preserving activation functions with Bjorck normalized layers (second row). We report Chamfer Distance (CD↓) and empirically estimated Lipschitz constant \(K_m\). Networks that approach the 1-Lipschitz budget more closely achieve better reconstruction quality.
Budget allocation experiments for 1-Lipschitz SDFs. Training with Householder (HH) and GroupSort (MaxMin) activations using Bjorck and SLL normalization shows that non-uniform allocation strategies perform on par with uniform approaches—suggesting the benefits may be stifled by the overly restrictive unit budget.
For lung CT registration, we derive the Lipschitz budget from clinical evidence: strain approaching 2.0 marks a threshold for tissue failure. This motivates our choice of \(K = 2\) as a principled, domain-driven budget.
Comparison of smoothness (Folding Ratio↓) and expressiveness (TRE↓) across Lipschitz-regularized INR architectures. Non-uniform allocations (e.g., exponential) can improve target registration error while maintaining comparable folding ratio to uniform allocation.
For image inpainting, we derive the Lipschitz budget using a data-driven oracle based on the maximum spectral norm of the image Jacobian. This provides an interpretable upper bound on expected signal variation.
Quantitative results for different allocation strategies in inpainting with FFNs. Performance peaks near the oracle estimate and degrades when the Lipschitz budget deviates, demonstrating the oracle provides a meaningful approximation.
Qualitative examples from CelebA inpainting. Non-uniform budget allocation strategies (First, Linear, Exponential) yield statistically significant improvements over uniform allocation, particularly near the oracle estimate (Distance=0).
Recent work shows that scaling SIREN weights by a factor \(\alpha\) improves accuracy and convergence. While existing explanations rely on NTK theory, we show that Lipschitz theory offers a complementary perspective: for a SIREN layer \(f(x) = \sin(\omega(\alpha \mathbf{W}x + b))\), the induced Lipschitz constant is \(\text{Lip}(f) = |\omega\alpha\|\mathbf{W}\||\), scaling linearly with \(\alpha\).
Visualization of the upper induced Lipschitz bound for weight scaling in SIREN. Scaling the initialization leads to direct scaling of layer Lipschitz bounds, allowing the network to increase its capacity for high-frequency content. Layer-wise analysis shows self-regulating capacity when weights are sufficiently scaled.
@inproceedings{mcginnis2026beyond,
title={Beyond Uniformity: Regularizing Implicit Neural Representations through a Lipschitz Lens},
author={Julian McGinnis and Suprosanna Shit and Florian A. H{\"o}lzl and Paul Friedrich and Paul B{\"u}schl and Vasiliki Sideri-Lampretsa and Mark M{\"u}hlau and Philippe C. Cattin and Bj{\"o}rn Menze and Daniel Rueckert and Benedikt Wiestler},
booktitle={International Conference on Learning Representations},
year={2026},
url={https://openreview.net/forum?id=XXXXX}
}
We thank Patricia Pauli for helpful discussions. This work is funded by the Munich Center for Machine Learning. Julian McGinnis and Mark Mühlau are supported by Bavarian State Ministry for Science and Art (Collaborative Bilateral Research Program Bavaria – Quebec: AI in medicine, grant F.4-V0134.K5.1/86/34). Suprosanna Shit is supported by the UZH Postdoc Grant (K-74851-03-01). Suprosanna Shit and Björn Menze acknowledge support by the Helmut Horten Foundation.